- Home
- ENERGIA
- Ricerca
- Ottimizzazione dello scambio termico nelle fasi di stiro e stabilizzazione del monofilamento in HDPE con forni ad acqua e ad aria
Ottimizzazione dello scambio termico nelle fasi di stiro e stabilizzazione del monofilamento in HDPE con forni ad acqua e ad aria
Nella produzione di monofilamenti in polietilene ad alta densità (HDPE), le fasi di stiro e stabilizzazione sono realizzate da forni con elevati consumi di energia termica e bassa efficienza. L’ottimizzazione dei processi può avvenire solo se vi è un’approfondita conoscenza dei fenomeni di trasmissione del calore tra fili e fluido circostante (aria o acqua). I coefficienti di scambio termico dipendono dalla distanza di separazione tra i filamenti che attraversano il forno, come dalla temperatura e dalla velocità relativa tra fili e fluido; le variazioni di questi parametri, se ben gestite nell’ambito di precisi range, consentono di agire efficacemente sulle dimensioni del forno e quindi sui consumi di energia termica.
Le simulazioni termofluidodinamiche condotte prendono in esame due particolari modelli commerciali di forno, uno ad acqua e l’altro ad aria. I risultati ottenuti evidenziano che una distanza di 2,5 mm tra i fili permette di massimizzare il coefficiente di scambio termico convettivo, pari a circa 5000 W/(m2 K) nel caso dell’acqua e a circa 470 W/(m2 K) per l’aria. La potenza necessaria a realizzare i processi è pari a circa 47 kW nel caso della vasca ad acqua e di 17 kW in quello del forno ad aria. Si osserva, dunque, che, per i due modelli di forno esaminati, anche se le condizioni di scambio termico dell’acqua sono molto migliori rispetto all’aria, la possibilità di adottare temperature più elevate di quest’ultima permette una riduzione della potenza totale: il modello di forno ad aria è alimentabile con una potenza pari a circa il 36% di quella necessaria al modello di vasca ad acqua.
1. Introduzione
Il polietilene ad alta densità (HDPE) è un polimero termoplastico semicristallino ottenuto per poliaddizione radicalica in massa del monomero di etilene [1, 2]. I suoi granuli vengono miscelati per ottenere le varie mescole e inviate a un estrusore, all’interno del quale il materiale viene rammollito alla temperatura di circa 280 °C, miscelato per garantire omogeneità di colore e di comportamento meccanico [3] e spinto attraverso una filiera dotata di fori di calibro noto. I filamenti appena estrusi attraversano una vasca di raffreddamento, dove subiscono la tempra necessaria a garantire la percentuale voluta di cristallinità al prodotto.
Il successivo processo è quello di stiro, che realizza un incremento di lunghezza del filo fino a quattro volte il valore iniziale e una strizione della sezione. In questa fase, il riscaldamento avviene in forni a temperatura controllata.
Dopo lo stiro, i fili subiscono un ulteriore trattamento termo-meccanico simile a quello appena descritto e detto di stabilizzazione. La geometria del forno di stabilizzazione è del tutto analoga a quella di stiro; la differenza risiede nella finalità di intervento sulla struttura del materiale.
Solidificatosi, i fili raggiungono un gruppo di ensimaggio. Qui viene applicata un’emulsione oleosa per migliorarne le proprietà funzionali nelle successive fasi successive di tessitura. I monofilamenti, infine, vengono avvolti in bobine in appositi dispositivi per la raccolta e l’uso sui telai [4].
Stiro e stabilizzazione sono effettuati con il ricorso di vasche ad acqua o, alternativamente, di forni ad aria. L’interesse dello studio condotto consiste nella possibilità di conseguire riduzioni non trascurabili della spesa energetica che, date le alte potenze termiche in gioco, configurerebbero riduzioni importanti di impatto ambientale di un processo produttivo (quello di produzione dei filati) fortemente energivoro.
Si tratta di affrontare analisi dei fenomeni su scale estremamente differenti, passando da valutazioni dello scambio termico del singolo filamento dal diametro di circa un quarto di millimetro a stime di potenze termiche fornite a volumi di fluidi nell’ordine del metro cubo. L’innovatività del metodo progettuale risiede, dunque, in un approccio che tiene conto da un lato delle esigenze di precisione nelle temperature raggiunte dai monofilamenti, dall’altro di quelle di impianto.
Se il metodo di studio, le considerazioni a monte dello stesso e le tecniche di simulazione termofluidodinamica sono estendibili alla maggior parte dei processi industriali descritti, i risultati, tuttavia, non possono assumere carattere generale, perché ottenuti prendendo in esame le geometrie e le caratteristiche tecniche di due tipologie di modello commerciale di forni.
2. Valutazione del coefficiente di scambio termico convettivo sui filamenti in HDPE
Le analisi delle geometrie e delle prestazioni delle macchine considerate sono precedute da una valutazione dello scambio termico al loro interno.
La temperatura alla quale devono essere portati i filamenti nei processi di stiro e stabilizzazione è compresa tra 65 e 70 °C. I valori più alti sono raggiunti durante la stabilizzazione e sono stati considerati come input delle simulazioni numeriche condotte.
Dal coefficiente di scambio convettivo sulle superfici del filamento vengono determinate le potenze termiche scambiate [5-7]. Dato il diametro dei monofilamenti (valore imposto dalle specifiche geometriche prodotto finito), la variabile geometrica che influenza la trasmissione del calore è la distanza tra i fili: il suo valore determina il regime di moto del fluido sui fili e, pertanto, ne condiziona le modalità di riscaldamento.
Le simulazioni condotte al variare della distanza tra i fili consentono la scelta del valore che massimizza il coefficiente di scambio termico medio [8]. Viene, quindi, simulato alternativamente il flusso di acqua e di aria che si instaura all’interno, rispettivamente, della vasca e dei canali del forno [9-11].
Il codice di calcolo utilizzato per le simulazioni numeriche di tipo CFD è Ansys Fluent v. 6.3.26 [12-15].
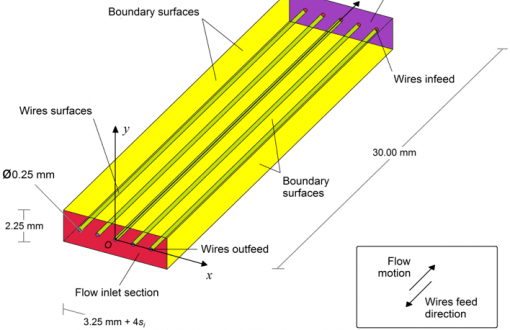
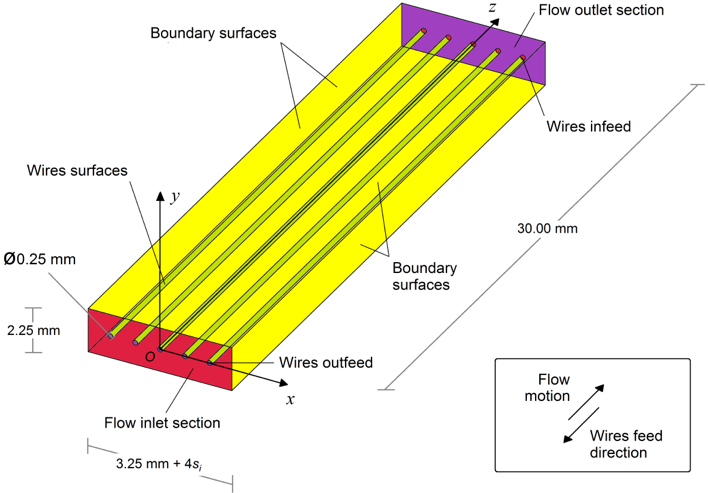
Il volume di controllo adottato (fig. 1) prevede la schematizzazione di cinque filamenti del diametro di 0,25 mm, ognuno dei quali è separato da quello adiacente da una distanza si variabile come in tab. 1. Dato, poi, che l’obiettivo è quello di valutare il coefficiente di scambio medio e poiché nel bagno di acqua o nei canali d’aria si riscontrano valori di velocità v e temperatura T del flusso a volte anche non omogenei, il calcolo è stato effettuato al variare di questi paramentri come in tab. 2.
I risultati mostrano che il coefficiente di scambio termico sulle superfici dei fili decresce esponenzialmente dalla sezione d’ingresso verso quella d’uscita e che il campo di variazione dei valori assunti all’interno del volume di controllo assume una configurazione concentrica e simmetrica rispetto all’asse del filo stesso. E’ possibile, dunque, considerare un valore di h locale medio sulla superficie di ogni filamento.
Il coefficiente h mediato su tutte le superfici dei filamenti varia notevolmente. I valori sono riassunti in tab. 2 sia nel caso dell’acqua, sia in quello dell’aria, insieme al valore medio di tutte le condizioni considerate.
Fig. 1: Modello di simulazione del flusso tra i filamenti
Tab. 1: Parametri di input per la stima del coefficiente di scambio termico convettivo
| Parametro | Valore | |
| Diametro del filo, d [mm] | 0,25 | |
| Distanza tra i filamenti, si [mm] | i = 1 | 0,25 |
| i = 2 | 1,0 | |
| i = 3 | 2,5 | |
| i = 4 | 3,3 | |
| i = 5 | 5,0 | |
Tab. 2: Condizioni di input delle simulazioni per ogni valore di si adottato
| Condizione | v [m/s] | T [°C] | Condizione | v [m/s] | T [°C] |
| a | 0,01 | 60 | f | 0,40 | 95 |
| b | 0,01 | 80 | g | 0,80 | 60 |
| c | 0,01 | 95 | h | 0,80 | 80 |
| d | 0,40 | 60 | i | 0,80 | 95 |
| e | 0,40 | 80 |
In generale, sia la temperatura, sia la velocità del fluido influiscono sul coefficiente di scambio termico convettivo; la prima variabile, tuttavia, dimostra di avere un’influenza maggiore.
Si osserva, inoltre, come i risultati mediamente peggiori in termini del coefficiente h si ottengano con si = 0,25 mm, seguito da si = 1,0 mm. I valori migliori si ottengono, invece, con si = 2,5 mm, mentre per si = 3,3 mm e si = 5,0 mm il coefficiente di scambio termico tende progressivamente a ridursi.
La spiegazione di ciò è da ricercarsi nel sempre minore disturbo tra loro dei filetti fluidi che lambiscono le superfici dei fili, all’aumentare della distanza di separazione. Questo andamento sembra, in ultimo, arrestarsi e invertirsi passando da si = 2,5 mm a si = 3,3 mm e a si = 5,0 mm. Il motivo sta nel fatto che, dal momento in cui ogni filo è circondato da un flusso indipendente da quello che circonda i fili vicini (senza che i campi di turbolenza dei relativi filetti fluidi interferiscano tra loro, smorzandosi), un ulteriore aumento di distanza di separazione provoca una sempre maggiore laminarizzazione del flusso che riduce lo scambio termico.
Si conclude, dunque, che la distanza ottima tra i filamenti risulta compresa nell’intorno dei 2,5 mm. In queste condizioni viene a massimizzarsi il coefficiente di scambio termico convettivo tra le superfici dei fili in lavorazione e il flusso di fluido che li lambisce, sia esso acqua o aria.
Tab. 3: Valori del coefficiente di scambio convettivo fluido-filamenti mediati sull’intera superficie al variare di si e delle condizioni di tab. 2 (nell’ultima riga sono riportate le medie di tutte le condizioni)
| Condizione | hmedio [W/(m2 K)] | ||||
| si = 0,25 mm | si = 1,0 mm | si = 2,5 mm | si = 3,3 mm | si = 5,0 mm | |
| Acqua | |||||
| a | 493,6 | 749,0 | 829,4 | 828,0 | 801,4 |
| b | 1480,5 | 2246,7 | 2488,0 | 2483,6 | 2405,1 |
| c | 2220,3 | 3369,9 | 3731,8 | 3725,3 | 3607,6 |
| d | 1570,0 | 1551,3 | 2133,9 | 2026,7 | 1954,3 |
| e | 4710,0 | 4654,0 | 6401,5 | 6080,0 | 5862,7 |
| f | 7064,9 | 6980,9 | 9602,2 | 9120,0 | 8794,1 |
| g | 1806,4 | 1818,3 | 2337,7 | 2195,2 | 2129,5 |
| h | 5419,1 | 5454,9 | 7012,9 | 6585,5 | 6388,3 |
| i | 8128,6 | 8182,4 | 10519,4 | 9878,3 | 9582,5 |
| Media delle condizioni | 3654,8 | 3889,7 | 5006,3 | 4769,2 | 4613,9 |
| Aria | |||||
| a | 17,2 | 26,8 | 31,0 | 31,0 | 30,2 |
| b | 171,5 | 268,4 | 309,8 | 309,3 | 301,8 |
| c | 342,9 | 536,8 | 619,6 | 617,9 | 601,7 |
| d | 35,7 | 42,9 | 48,5 | 48,5 | 47,6 |
| e | 354,9 | 440,2 | 484,6 | 484,8 | 476,5 |
| f | 709,3 | 880,4 | 968,7 | 969,2 | 952,9 |
| g | 44,2 | 49,6 | 58,0 | 58,0 | 56,4 |
| h | 439,3 | 496,1 | 580,4 | 577,0 | 564,2 |
| i | 878,3 | 992,2 | 1.159,0 | 1153,9 | 1.128,3 |
| Media delle condizioni | 332,9 | 414,8 | 473,3 | 472,2 | 462,2 |
3. Valutazione delle prestazioni della vasca ad acqua
La macchina presa in considerazione è la vasca ad acqua illustrata in fig. 2. Costruttivamente, dispone, nella parte inferiore, di una pompa per il ricircolo del fluido e di n. 18 resistenze elettriche capaci di mantenere il bagno isotermo alla temperatura desiderata. Uno schema esemplificativo della vasca ad acqua è riportato in fig. 3.
Dal fondo, l’acqua risale l’involucro sino a colmarlo e a bagnare integralmente i filamenti, raggiunge la parte superiore della vasca (delimitata dalla sagoma in rosso) passando attraverso i due fori sormontati da cupole al fine di evitare eventuali schizzi verso l’alto, e, muovendosi verso le superfici esterne nella vista frontale e superiore, stramazza dai pozzetti di estremità per tornare nella parte inferiore ed essere nuovamente riscaldata e ricircolata dalla pompa. La velocità del fluido è ridotta e tale da mantenere il bagno a temperatura costante.
A causa della particolarità costruttiva della vasca, consistente nel possedere due fori di ingresso dell’acqua riscaldata di dimensioni limitate se comparate con quelle dell’intero profilo, i risultati della simulazione numerica mostrano un forte incremento della temperatura dei filamenti localizzato nei pressi delle superfici di ingresso. A questo si accompagna una visibile riduzione della temperatura degli stessi nelle parti centrali del profilo, zone in cui lo spessore del bagno fluido è ridotto. Nelle sezioni di uscita dei filamenti, infine, la loro temperatura si stabilizza sul valore desiderato. In fig. 4 si osserva quanto descritto.
Questa modalità di riscaldamento dei filamenti di tipo “a due stadi” è spiegabile anche studiando il campo della velocità dell’acqua all’interno della vasca. Dalla fig. 5 si osserva come i valori siano massimi nelle zone di ingresso e uscita e si verifichi un ristagno nelle zone centrali a sezione di passaggio ridotta.
Oltre a ciò, data la direzione di scorrimento dei filamenti, si verifica anche un trascinamento del fluido verso le zone di uscita dei fili. Questo aspetto risulta benefico per lo scambio termico; ciò a causa di un maggior tempo di contatto tra l’acqua calda in ingresso e i fili stessi durante il loro attraversamento della vasca.
Fig. 2: Vasca ad acqua (costruttore: OMGM sas)

Fig. 3: Schema esemplificativo della vasca ad acqua con indicazione degli ingombri
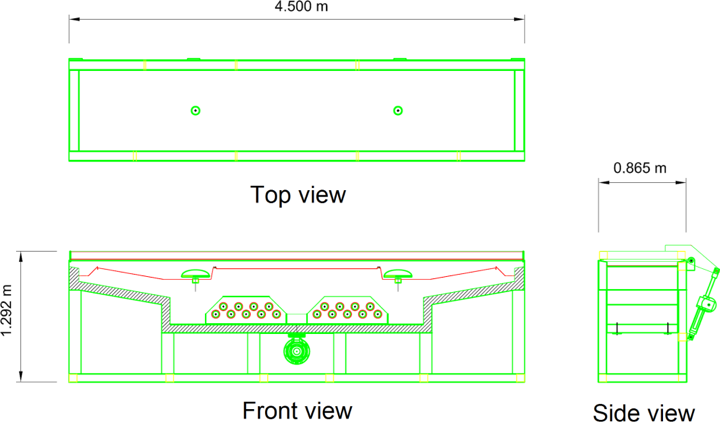
Fig. 4: Campo di temperatura all’interno della vasca
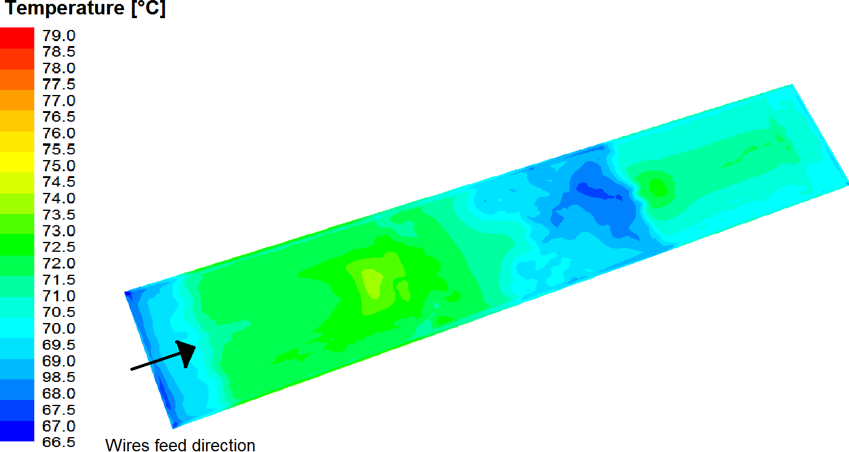
Fig. 5: Campo di velocità del fluido

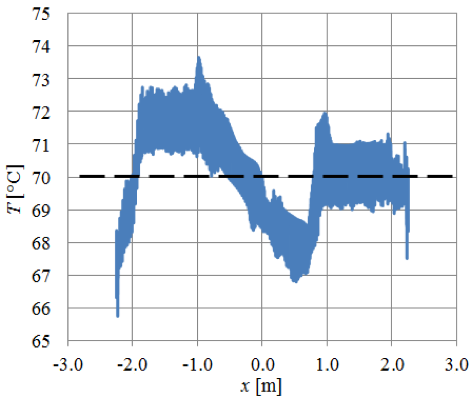
In fig. 6 è descritto l’andamento della temperatura media del fluido nella direzione di scorrimento. Una linea tratteggiata identifica il valore di 70 °C; si osservi come nella sezione di uscita i filamenti presentino una temperatura media proprio pari al valore desiderato.
Il processo di riscaldamento simulato comporta la necessità di garantire una portata di acqua pari a 2 kg/s (che implica una velocità media del flusso di 0,099 m/s), con una temperatura d’ingresso nel profilo simulato di 78,0 °C e di uscita di 72,4 °C (temperatura media del bagno: 74,0 °C). La perdita di carico totale tra ingresso e uscita è di circa 45 Pa. Ciò implica un fabbisogno di potenza termica (alle resistenze) pari a 46,98 kW e di potenza meccanica (alla pompa) trascurabile.
Fig. 6: Temperatura dei fili al variare della sezione di passaggio nella vasca ad acqua
4. Valutazione delle prestazioni del forno ad aria
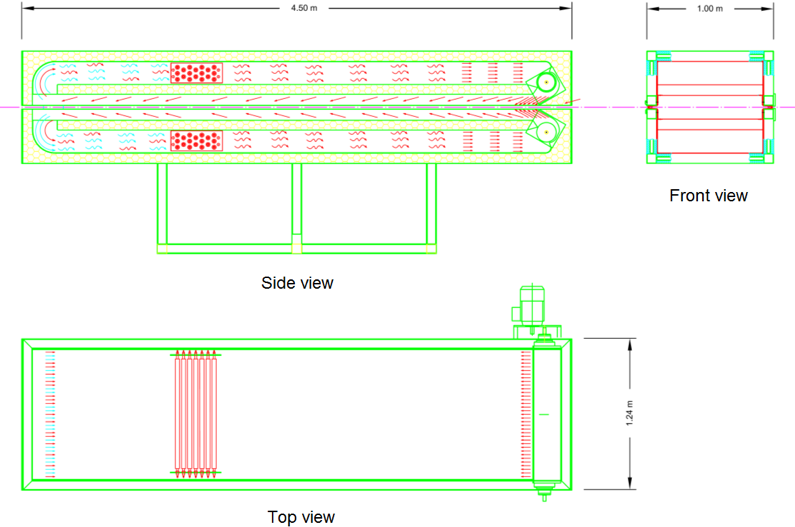
Il forno ad aria considerato è illustrato nella fotografia di fig. 7 ed è schametizzato in fig. 8. Si compone di due canali separati e sovrapposti, all’interno dei quali il flusso d’aria generato da due ventilatori tangenziali viene riscaldato da un pacco di n. 18 resistenze elettriche e lambisce i filamenti di HDPE in lavorazione (posti sulla linea di mezzeria del forno).
Fig. 7: Forno ad aria (costruttore: OMGM sas)

Al fine di ottimizzare l’impiego delle risorse computazionali, il modello da simulare è stato scomposto in due sottocomponenti: la sezione contenente il pacco delle resistenze e quella che lambisce i filamenti.
I risultati della simulazione relativa al secondo mostrano, in fig. 9, un progressivo raffreddamento dell’aria mentre lambisce i filamenti. Il maggior calo termico si verifica in corrispondenza delle perdite/rientrate di fluido nelle zone di ingresso e uscita dei fili (nelle zone estreme a destra e a sinistra del relativo modello). In termini di potenza dissipata, comunque, sono i filamenti in riscaldamento a generare la quota maggiore, seguiti dalle pareti esterne del forno a contatto con l’ambiente.
Fig. 8: Schema del forno ad aria con indicazione degli ingombri
| Flow direction |
Fig. 9: Campi di temperatura per i modelli dei condotti di circolazione del forno ad aria
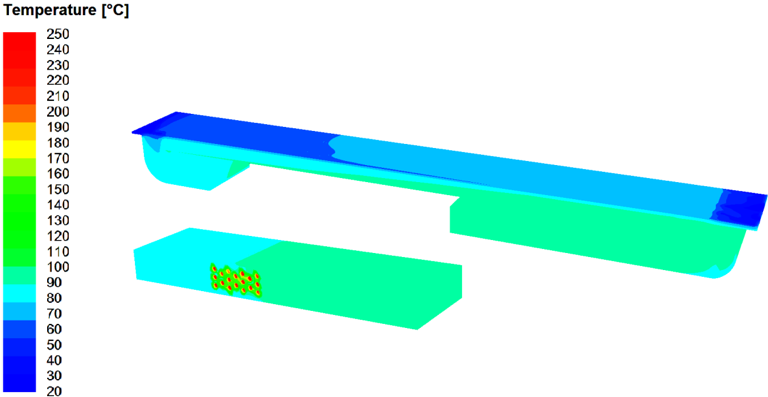
Per ciò che concerne, invece, il campo di temperatura nei pressi delle resistenze elettriche, si distinguono chiaramente le zone ad elevata temperatura delimitate dalle stesse resistenze e la scia di flusso riscaldato che si propaga verso la sezione d’uscita.
A livello dei campi di velocità dell’aria all’interno del canale, invece, le simulazioni mostrano che i valori maggiori sono raggiunti in corrispondenza delle curve e in prossimità delle resistenze [16]. La portata d’aria necessaria a garantire il riscaldamento dei fili sino a 70 °C è di 2,8 kg/s e permette di generare un flusso uniforme su tutta la loro superficie, rendendo contenuta la turbolenza e riducendo, dunque, a un livello accettabile le perdite di carico prodotte. Questo valore di portata massica comporta la necessità di garantire una potenza termica alle resistenze di 14,8 kW (con temperature del fluido a monte di 88,4 °C e a valle di 93,4 °C) e una potenza meccanica ai ventilatori di 2,2 kW. La perdita di carico complessiva è pari a 276,6 Pa.
5. Confronti e conclusioni
Nel processo produttivo del monofilamento in HDPE, le fasi di stiro e stabilizzazione richiedono un fabbisogno di energia termica consistente. Per questo, è stata condotta una campagna di simulazioni termofluidodinamiche con l’obiettivo di investigare sulle condizioni termiche ottimali all’interno dei forni, massimizzando il coefficiente di scambio termico convettivo medio sulla superficie dei filamenti e stimando le potenze termica e meccanica nel caso di impiego di acqua o aria come fluido di riscaldamento.
Le analisi relative al coefficiente di scambio convettivo sono state condotte al variare della distanza di separazione tra i fili, variabile che non influenza le specifiche del prodotto finito e, come tale, liberamente modificabile. Il peggiore coefficiente h si ottiene con si = 0,25 mm, seguito da si = 1,0 mm. All’aumentare di si, dunque, cresce h. L’andamento, tuttavia, si arresta e si inverte passando da si = 2,5 mm a si = 3,3 mm e a si = 5,0 mm. Alle ridotte distanze di separazione, un aumento produce un sempre minore disturbo tra di loro dei filetti fluidi che lambiscono le superfici dei fili; così, per alcuni valori della distanza, ogni filo viene circondato da un flusso indipendente da quello che circonda i fili vicini, senza che i campi di turbolenza dei relativi filetti fluidi interferiscano tra loro, smorzandosi. Un ulteriore aumento di distanza di separazione, tuttavia, provoca una sempre maggiore laminarizzazione del flusso, che riduce lo scambio termico.
La distanza ottima tra i filamenti è nell’intorno di 2,5 mm. In queste condizioni il coefficiente di scambio termico convettivo sulle superfici dei fili è pari a 5006,3 W/(m2 K) nel caso dell’acqua e a 473,3 W/(m2 K) in quello dell’aria. Senza dubbio, il confronto tra i due fluidi di riscaldamento premia il primo: a parità di condizioni al contorno, lo scambio termico convettivo risulta più di 10 volte maggiore rispetto al secondo.
I valori del coefficiente di scambio così determinati sono stati utilizzati nella simulazione delle caratteristiche dei due modelli di forno presi in esame. I risultati ottenuti in termini di prestazioni energetiche nel caso della vasca ad acqua e in quello del forno ad aria sono riassunti in tab. 4.
Tab. 4: Prestazioni energetiche della vasca ad acqua e del forno ad aria
| Parametro | Vasca ad acqua | Forno ad aria |
| Temperatura media, T [°C] | 74,0 | 90,9 |
| Portata massica, [kg/s] | 2,0 | 2,8 |
| Perdita di carico, Δp [Pa] | 45,0 | 276,6 |
| Potenza termica resistenze, [kW] | 46,98 | 14,80 |
| Potenza meccanica ventilatori, P [kW] | ~ 0,00 | 2,20 |
| Potenza totale, [kW] | 46,98 | 17,00 |
Anche se le condizioni di scambio termico dell’acqua sono migliori rispetto all’aria, la possibilità di adottare temperature più elevate di quest’ultima permette una riduzione della potenza necessaria: il forno ad aria è alimentabile con una potenza pari a circa il 36% rispetto alla vasca ad acqua. I risparmi in termini di consumi energetici sono, dunque, molto rilevanti. Anche in considerazione del fatto che, nella maggior parte dei casi, sia l’energia termica che quella meccanica sono generate elettricamente.
Il calo dei fabbisogni elettrici e le maggiori temperature medie all’interno del forno ad aria conducono, di conseguenza, anche alla possibilità di ridurre gli ingombri della macchina e, dunque, il costo dei materiali di produzione e il peso.
Ringraziamenti
Si ringrazia l’azienda Sachim srl, produttrice di reti in HDPE, che, nell’ambito del progetto Tessuti a rete innovativi per uso agricolo – a valere sui Pacchetti integrati di agevolazione (PIA) per Medie Imprese e ai Consorzi di PMI - Titolo V del regolamento generale dei regimi di aiuto in esenzione - Reg. reg. 26 giugno 2008, n.9 - Avviso 2008- Programma Operativo FESR 2007 – 2013, ha consentito lo svolgimento delle attività di studio.
Bibliografia
[1] Lindsey C.R., Paul D.R., Barlow J.W. (1981), Mechanical Properties of HDPE–PS–SEBS Blends, Journal of Applied Polymer Science, 26(1), 1-8.
[2] Zhang X.M., Elkoun S., Ajji A., Huneault M.A. (2004), Oriented Structure and Anisotropy Properties of Polymer Blown Films: HDPE, LLDPE and LDPE, Polymer, 45(1), 217-229.
[3] Zou Y., Feng Y., Wang L., Liu X. (2004), Processing and Properties of MWNT/HDPE Composites, Carbon, 42(2), 271-277.
[4] Dassisti M., Intini F., Chimienti M., Starace G. (2016), Thermography-Enhanced LCA (Life Cycle Assessment) for Manufacturing Sustainability Assessment. The Case Study of an HDPE (High Density Polyethylene) Net Company in Italy, Energy, 108, 7-18.
[5] Rohsenow W.M., Hartnett J.P., Cho Y.I. (1998), Handbook of Heat Transfer, 3rd ed., McGraw-Hill, New York.
[6] Rohsenow W.M., Hartnett J.P., Ganic E.N. (1985), Handbook of Heat Transfer Applications, 2nd ed., McGraw-Hill, New York.
[7] Kakaç S., Shah R.K., Aung W. (1987), Handbook of Single-Phase Convective Heat Transfer, John Wiley and Sons, New York.
[8] Minkowycz W.J., Sparrow E.M., Murthy J.Y. (2006), Handbook of Numerical Heat Transfer, 2nd ed., John Wiley and Sons, New York.
[9] Alizadehdakhela A., Rahimia M., Alsairafib A.A. (2010), CFD Modeling of Flow and Heat Transfer in a Thermosyphon, 37(3), 312-318.
[10] Zhai Z.J., Zhang Z., Zhang W., Chen Q.Y. (2007), Evaluation of Various Turbulence Models in Predicting Airflow and Turbulence in Enclosed Environments by CFD. Part 1: Summary of Prevalent Turbulence Models, HVAC&R Research, 13(6), 853-870.
[11] Zhai Z.J., Zhang Z., Zhang W., Chen Q.Y. (2007), Evaluation of Various Turbulence Models in Predicting Airflow and Turbulence in Enclosed Environments by CFD. Part 2: Comparison with Experimental Data from Literature, HVAC&R Research, 13(6), 871-886.
[12] Ansys Fluent v. 6.3.26, http://www.ansys.com/Products/Simulation+Technology/Fluid+ Dynamics/
[13] Pletcher R.H., Tannehill J.C., Anderson D.A. (2013), Computational Fluid Mechanics and Heat Transfer, 3rd ed., CRC Press, Boca Raton.
[14] Guardo A., Coussirat M., Larrayoz M.A., Recasens F., Egusquiza E. (2005), Influence of the Turbulence Model in CFD Modeling of Wall-to-Fluid Heat Transfer in Packed Beds, Chemical Engineering Science, 60(6), 1733-1742.
[15] Amano R.S., Sundén B. (2011), Computational Fluid Dynamics and Heat Transfer, WIT Press, Billerica.
[16] Starace G., Fiorentino M., Longo M.P., Carluccio E. (2017), A Hybrid Method for the Cross Flow Compact Heat Exchangers Design, Applied Thermal Engineering, 111, 1129-1142.
Articoli correlati

[30.10.20] Il brevetto a supporto dell'innovazione

[03.04.18] AAA efficienza energetica cercasi

[12.07.17] Ecobonus traino dell’efficienza energetica